Introduction
It is well known that helices and ß-sheets are the major stabilizing structures in proteins. Segments of the protein chain which are not helical nor ß-sheet have been generally designated as random coil or irregular regions. These nonrepetitive motif elements include tight turns, bulges, and random coil structures (Richardson, 1981).
Tight Turns
There are different types of tight turns (Chou 2000) depending upon the number of atoms forming the turn. These are as follows:
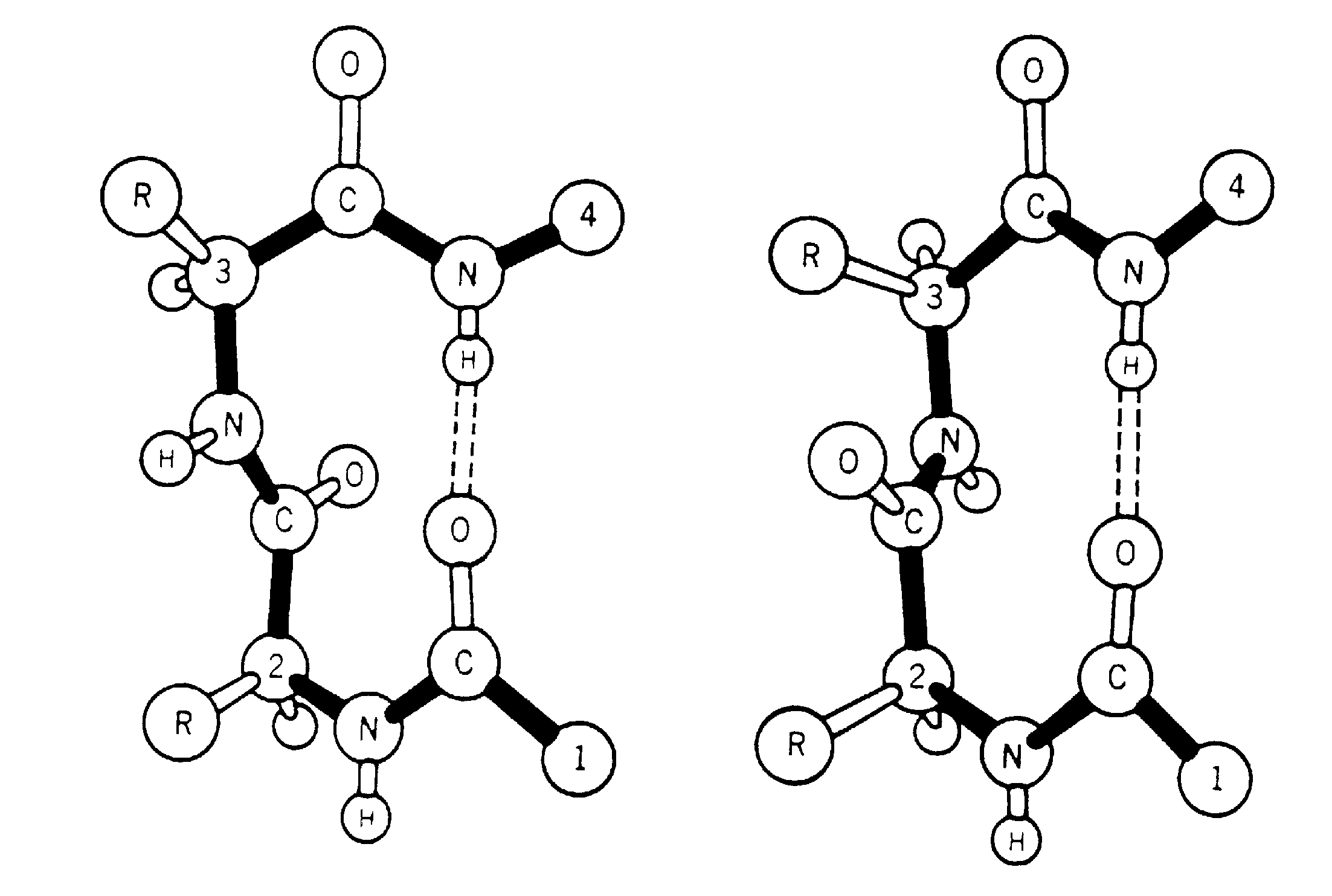
A ß-turn is a region of the protein involving four consecutive residues where the polypeptide chain folds back on itself by nearly 180 degrees (Lewis et al. 1971, 1973; Kuntz,1972; Crawford et al.,1973; Chou & Fasman ,1974). It is these chain reversals which give a protein its globularity rather than linearity.
The ß-turn was originally identified, in model building studies, by Venkatachalam (1968). He proposed three distinct conformations based on phi,psi values (designated I,II and III) along with their related turns (mirror images) which have the phi, psi signs reversed (I',II' and III'), each of which could form a hydrogen bond between the main chain C=O(i) and the N-H(i+3). Subsequently, Lewis et al. (1973) examined the growing number of three-dimensional protein structures and suggested a more general definition of a ß-turn. This stated that the distance between the Calpha(i) and the Calpha(i+3) was <7Å and the residues involved were not helical. They found that 25% of their extended ß-turns did not possess the intraturn hydrogen bond suggested by Venkatachalam. To include the new data they extended the classification of ß-turns to 10 distinct types (I,I',II,II',III,III',IV,V,VI and VII). These classes were defined not only by phi,psi angles, but also less stringent criteria. Richardson (1981) has since reappraised the situation, and has suggested that there are only 6 distinct types (I,I',II,II',VIa and VIb) based on phi,psi ranges, along with a miscellaneous category IV. The Richardson classification is the system most widely used at present. Two main types of ß-turns are Type-I and Type-II with their mirror images I' and II'.

Two types of ß-turns (Type-I and Type-II)
A ß-turn consists of four consecutive residues defined by positions i, i+1, i+2, i+3 which are not present in alpha-helix; the distance between Calpha(i) and Calpha(i+3) is less than 7Å (Richardson 1981; Rose et al. 1985) and the turn leads to reversal in the protein chain. ß-turns may or may not be accompained by the NH(i+3)-CO(i) hydrogen bond connecting the main chain atoms; CO of the ith residue and NH of (i+3)rd residue in the turn (Lewis et al 1973; Nemethy and Scheraga 1980).
Turns play an important role in globular proteins from both structural and functional points of view. A polypeptide chain cannot fold into a compact structure without the component of turns. Also, turns usually occur on the exposed surface of proteins and hence probably represent antigenic sites or involve molecular recognition. Thus, owing to the above reasons, the prediction of ß-turns in proteins is an important element of secondary structure prediction.
Prediction Algorithms
Various methods for prediction of tight turns and their types are reviewed by Chou. The existing prediction methods can be classified into 3 categories:
There are various approaches for the prediction of ß-turns (Lewis et al. 1973; Chou & Fasman 1974; Garnier et al. 1978; Chou & Fasman 1979; Cohen et al. 1986; Wilmot & Thornton 1988; McGregor et al. 1989; Chou 1997; Zhang & Chou 1997; Chou & Blinn 1997).
Site-Independent Model
This model is based upon the knowledge of amino acid preferences at individual positions in ß-turns and does not consider any coupling between the residues in the sequence. A simple empirical method based on this concept was first introduced by Lewis et al. (1971) and Chou-Fasman (1977). All these methods described below involves no coupling between the residues forming the turn and thus can be classified as Site-Independent Models.
Chou-Fasman algorithm : It was based on calculating the product of derived amino acid probabilities at each of the four positions in the turn and calculating positional frequencies and conformational parameters.
Thornton's algorithm : Later, the conformational potentials, positional potentials and turn type dependent positional potentials were recalculated by Hutchinson & Thornton in 1988 by using a dataset of 59 proteins for the prediction of Type I and II ß-turns.
GORBTURN(v3.0) : In 1990, a ß-turn prediction program called GORBTURN (v 1.0) was developed by using the directional parameters of Gibrat et al. in combination with equivalent parameters produced from work by Garett et al. to eliminate potential helix and strand forming residues from the ß-turn prediction. Later in 1994, the program GORBTURN (v 1.0) was improved by incorporating the positional frequencies as calculated by Thornton by using a dataset of 205 protein chains and finally a new version of GORBTURN(v3.0) was developed for the prediction of different types of ß-turns (Type I, I', II, II', VIII and non-specific). In 1997,
1-4 & 2-3 Correlation Model
In 1997, an entirely new model, the so-called 1-4 & 2-3 correlation model was proposed by Chou to predict the ß-turns in proteins based on residue coupling. In this model, the coupling effect between the 1st and the 4th residues and that between the 2nd and the 3rd residues was given a special consideration.
Sequence Coupled Model
In the same year i.e. 1997, a sequence coupled model was proposed by Chou for prediction of ß-turns in proteins. It was based on first-order markov chain involving conditional probabilities. These 1-4 & 2-3 correlation model and sequence coupled model were confined to ß-turn and non-turn, i.e., it can be used to predict one of only two possibilities. So, in the same year, Chou & Blinn extended the sequence coupled model for the prediction of different types of ß-turns (Type I, I', II, II', VI, VIII).